Research

The aim of this master's thesis is to apply up-to-date numerical methods for the efficient simulation of bearing elements.

Investigators: M. Bebendorf, T. Rau
Funded by Schaeffler AG, Herzogenaurach
Duration: October 2018 - April 2019

In many applications from physics, engineering and economy, non-local operators are used to model the respective phenomenon. Such operators are characterised by the property that each output datum depends on each input datum when the operator is applied to a data set. Examples are integral operators arising from the boundary integral method, the Gauss transform, the Lippmann-Schwinger equation in quantum perturbation theory, non-integer powers and the inverse of differential operators. Also integral operators for modelling Levy processes in risk management belong to this class. Their discretization leads to fully populated matrices which due to the underlying geometry or the desired accuracy of the solution are large scale in general. Already storing such matrices can be a problem. However, the numerical solution of linear systems in which they appear as a coefficient matrix can currently not be done in acceptable time. In this project a new approach for the efficient numerical treatment of non-local operators will be developed and investigated. Both, the fast multipole method and hierarchical matrices can be employed to treat large scale discretizations of such operators with logarithmic-linear complexity. Depending on the respective method, the operator is approximated locally or blockwise with the prescribed accuracy. The resulting approximation is universally applicable to any right hand side of linear systems in which it appears as a coefficient matrix. If many systems with the same operator are to be solved, then this kind of approximation is particularly efficient. However, often (probably in most cases) only a single system is to be solved for one operator, because it may, for instance, change in the course of a simulation. In such a situation, the universality of the approximation cannot be taken advantage of. On the contrary, the universality is paid for by generating and storing dispensable information. Since there are currently few alternatives, this kind of approximation is still used in practise. The aim of this project is to improve this situation by developing a new technique which tailors the approximation to the right hand side. Both, fast multipole methods and hierarchical matrices will be able to benefit from this new approach. Hence, succesful and widely recognised methods will be extended to significant problems to which they have not been efficiently applicable yet.

​investigators: M. Bauer, M. Bebendorf
funded by DFG via individual grant
duration: May 2016 - April 2019

Producing accurate simulations of ocean, atmosphere, and climate applications requires very efficient numerical schemes and huge computational resources not readily available in many parts of the world and to many groups active in this field. Such limitations also play a significant role in the fact that structured grid models still constitute the mainstay for community codes in the area of ocean science. In this project, we propose both to significantly improve the computational performance of unstructured grid ocean applications - focusing on a solver based on the discontinuous Galerkin finite element method - and, at the same time, to decrease the effort to implement new methods and applications. The first goal will be reached by utilizing a number of techniques aiming to address the existing performance bottlenecks; those include a new approach to domain decomposition and performance oriented adaptive numerical schemes. The second goal will be achieved by resorting to modern software design strategies, including code generation and automatic optimization techniques for the compute-intensive kernels. The performance and code design advances resulting from the work proposed here can cover a lot of ground towards making unstructured mesh models the mainstream of ocean science and, in particular, available to users with limited access to HPC systems.

​Investigators: Sara Faghih-Naini, Vadym Aizinger
Funding: DFG via individual grant
Duration: 2016 - 2020

The mathematical simulation of many physical processes in different areas of science and engineering leads to partial differential equations with stochastic coefficients. Usually, the discretization of the stochastic PDE results in parameterized deterministic PDEs, where the statistical properties of the random input data determine the dimension of the parameter space. If the dimension is small we aim at applying hierarchical matrix based solvers due to its robustness with respect to the deterministic operator's coefficients. Furthermore, this structure allows to exploit similarities between the systems. If the parameter space is high-dimensional, data-sparse representations (i.e. tensor approximations) of the unknowns and the given data are required. Here, recent high-dimensional generalizations of the adaptive-cross approximation method can be used.

investigators: M. Bebendorf, R. Venn
funded by DFG via project B07 in CRC 1060 The Mathematics of Emergent Effects
duration: January 2013 - June 2015

Im Rahmen des Projektes werden Fragestellungen aus dem Bereich der effektiven adaptiven Approximation von tensorwertigen Daten bearbeitet, die insbesondere bei der numerischen Modellierung und Lösung von parameterabhängigen mehrdimensionalen Integralgleichungen entstehen. Beispielhaft werden dazu Streuprobleme akustischer und elektromagnetischer Wellen betrachtet, wobei die Wellenzahl der zusätzliche Parameter ist. Zur numerischen Behandlung eignet sich die Randelementmethode. Diese führt auf vollbesetzte komplexwertige Matrizen, die ohne eine effektive Approximation nicht bearbeitet werden können. Besonders schwer wird die Situation, wenn, wie in der Praxis oft der Fall, ein ganzes Spektrum von Frequenzen (10^2-10^4) von Interesse ist. Während die Approximation einzelner vollbesetzter Matrizen seit Ende der 90er Jahre als ACA-Methode (``Adaptive Cross Approximation'') entwickelt wurde und inzwischen weltweit benutzt wird, steht die Entwicklung entsprechender Approximationsmethoden für drei- und allgemein mehrdimensionale Daten dagegen noch aus und bildet den ersten und wichtigsten Schwerpunkt des Projekts. Der zweite Schwerpunkt ist die BEM für Multifrequenzstudien von Streuproblemen für die Helmholtz-Gleichung, der dritte Schwerpunkt bildet die entsprechenden elektromagnetischen Streuprobleme. Besonders bei letzteren sind die Multifrequenzstudien für beide Grenzfälle (niedrige und hohe Frequenzen) nichttrivial und führen auf Gleichungssysteme, die wegen einer extrem schlechten Kondition oft eine Herausforderung darstellen.

investigators: M. Bebendorf, A. Kühnemund
funded by DFG via individual grant
​duration: November 2010 - October 2013

The aim of this project is to investigate a new approach to preconditioning finite element discretizations of differential operators by hierarchical matrix approximations. In order to improve their efficiency, approximations to eigenspaces corresponding to small eigenvalues will be preserved by exploiting multiscale eects. The new method will be used for the efficient simulation of singular phenomena in micromagnetics. New formulations of the stray field energy functional will allow to develop fast techniques for computing stable congurations and minimum energy paths between them. Furthermore, up-to-date methods will be developed for treating reduced 2-d models and time-dependent problems.

investigators: M. Bebendorf, M. Bratsch
funded by DFG via CRC 611 Singular Phenomena and Scaling in Mathematical Models
duration: June 2009 - December 2012

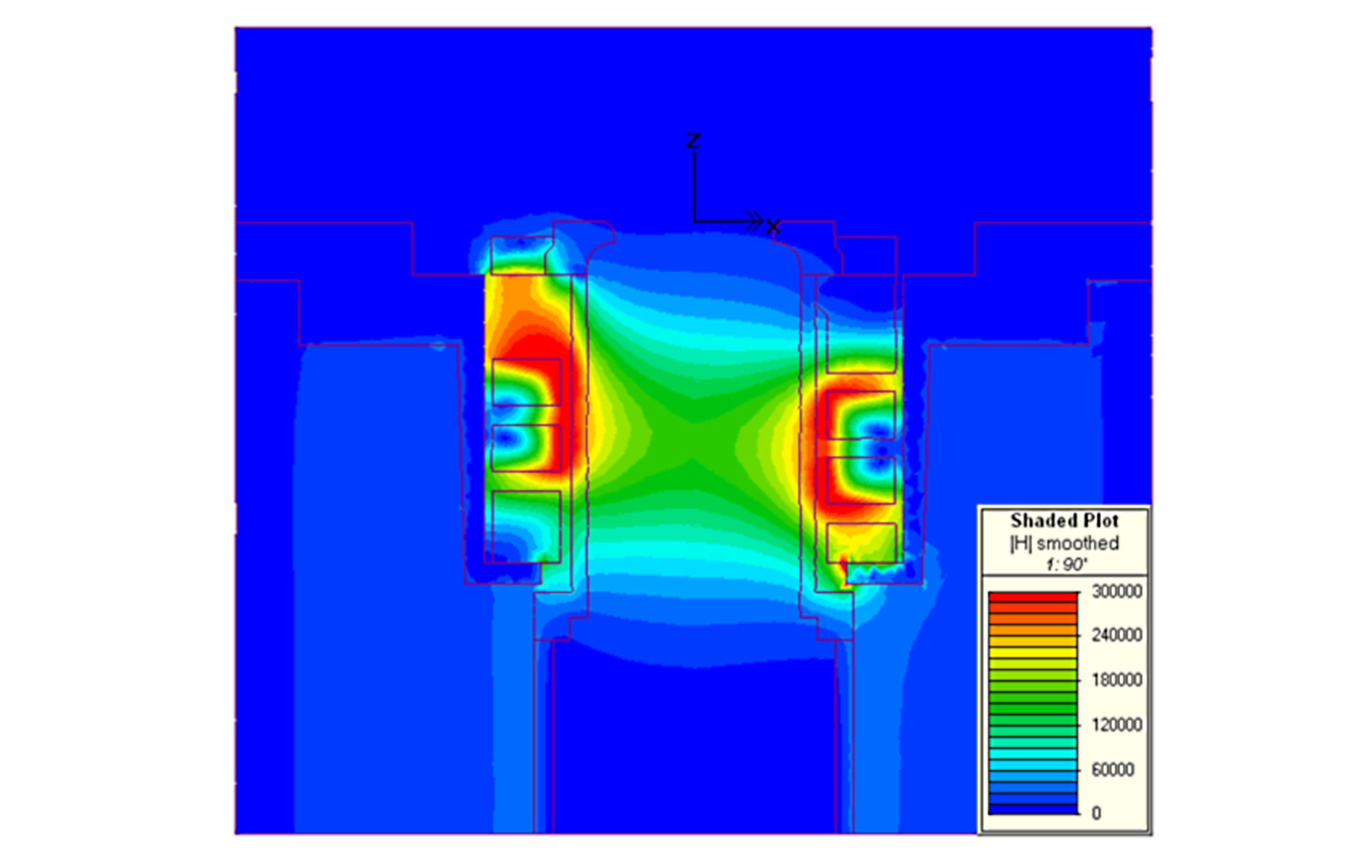
Series of projects concerned with the application of hierarchical matrices to real-world electromagnetic problems.

principal investigator: M. Bebendorf
funded via cooperation contract with ABB Switzerland AG
duration: April 2004 - March 2012

Bei der iterativen Lösung von in Folge der Finite-Elemente-Methode auftretenden linearen Gleichungssystemen ist wegen der asymptotisch schlechten Kondition der Systemmatrix eine Vorkonditionierung nötig. Die Koeffizienten der zur Modellierung inkrementeller Umformverfahren verwendeten partiellen Differentialgleichungen sind stark veränderlich, so dass sich die etablierten Vorkonditionierungstechniken wie Mehrgitterverfahren oder BPX insbesondere wegen der fehlenden Gitterhierarchie für diese Anwendung nicht eignen. Im Projekt werden die für ihre Robustheit bekannten hierarchischen Matrizen auf Probleme der Umformtechnik angewendet.

investigators: M. Bebendorf, Y. Chen, T. Fischer
funded by DFG via priority program 1146 Modelling of incremental forming processes
duration: October 2003 - August 2009